Conditions for rhombuses rectangles and squares – Delving into the realm of geometry, we embark on an exploration of the conditions that govern the classification of rhombuses, rectangles, and squares. These fascinating shapes, each possessing unique characteristics, form a hierarchical relationship that reveals their interconnectedness and shared properties.
As we unravel the intricacies of these quadrilaterals, we will uncover the geometric principles that define their form and behavior, providing a comprehensive understanding of their essential features.
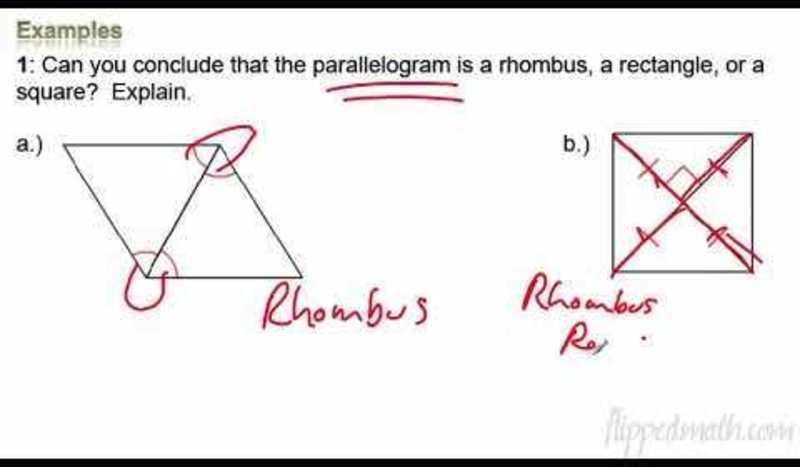
Definition of Rhombuses, Rectangles, and Squares

In geometry, a rhombus is a quadrilateral with four equal sides. A rectangle is a quadrilateral with four right angles. A square is a quadrilateral with four equal sides and four right angles.
Properties of Rhombuses
- Diagonals bisect each other perpendicularly.
- Diagonals are perpendicular to sides.
- Opposite angles are congruent.
Properties of Rectangles, Conditions for rhombuses rectangles and squares
- Opposite sides are parallel and congruent.
- Diagonals are congruent.
- All angles are right angles.
Properties of Squares
- All sides are congruent.
- All angles are right angles.
- Diagonals are perpendicular and bisect each other.
Relationships between Rhombuses, Rectangles, and Squares
Squares are a special type of rectangle, which in turn is a special type of rhombus. This means that all squares are rhombuses and rectangles, and all rectangles are rhombuses.
Quick FAQs: Conditions For Rhombuses Rectangles And Squares
What is the defining characteristic of a rhombus?
A rhombus is a quadrilateral with four equal sides.
How can you identify a rectangle?
A rectangle is a quadrilateral with four right angles.
What is the relationship between a square and a rectangle?
A square is a rectangle with four equal sides.